Figuuride kuvamine tasapinnal (definitsioon)

2024 Autor: Leah Sherlock | [email protected]. Viimati modifitseeritud: 2023-12-17 05:33

Oskus õigesti kuvada erinevaid kujundeid lehe, lõuendi ja mis tahes muu pinna tasapinnal on üsna oluline oskus. Ja ennekõike on see oluline nii kunstiinimestele: maalijatele, skulptoritele, graafikutele, disaineritele (siseruumide ja arhitektuurse keskkonna kujundajatele) kui ka teadustöötajatele: matemaatikutele, füüsikutele, disaineritele, leiutajatele.

Kuid nendest sfääridest kaugel viibival inimesel on oluline ka õppida ümbritsevat maailma õigesti tajuma ja kuvama. See aitab palju sügavam alt mõista selle mitmekülgsust. Kui teil pole piisav alt ettekujutust, kuidas seda õigesti teha, siis tõenäoliselt ei õnnestu teil ühegi leiutise projekti, pildi või joonisega. See tähendab, et see oskus on oluline nii lihtsate igapäevaste ülesannete lahendamisel kui ka nende jaoks, millel on globaalne, universaalne tähendus.

Natuke ajalugu

Iidsetest aegadest on inimesed püüdnud kujutada seda, mida nad enda ümber nägid: teisi inimesi, tolle aja ürgseid ehitisi, hämmastav alt kaunist taimede ja loomade maailma, majesteetlikke mägesid ja lihts alt asju, majapidamistarbeid. See tähendab, maailm kogu selle mitmekesisuses ja suursugususes.

Aga siis polnud neil veel õrna aimugi, kuidas seda täpselt ja asjatundlikult teha nii, et erinevate kolmemõõtmeliste objektide kuvamine lennukis oleks tõesti realistlik, elav. Inimesel puudusid vastavad teadmised ja pealegi polnud ka erilisi oskusi, välja arvatud ehk kõige elementaarsemad.

Varasemates allikates on öeldud, et maailma esimene maal koosnes vaid ühest joonest, mis kulges mööda päikese poolt seinale heidetud inimese varju. See tähendab, et loodus soovitas ise, mis suunas tasub sellele probleemile õiget lahendust otsides liikuda.

Ja see küsimus muretses tollase mehe ka sel põhjusel: ta ei tahtnud lihts alt imetleda mahukat elavat siluetti, nii-öelda originaali, vaid püüdis tabada ruumilist objekti tasapinnal. Ja ta tegi seda selleks, et sel viisil saaks kaunistada oma kodu või talle püha kohta või võtta kaasa pildiga kimp ja seda igale poole liigutada.

Mustri geomeetria

Ja mida iganes sa ütled, aga möödusid aastad, möödusid sajandid ja millegipärast õppisid inimesed tsivilisatsiooni arenedes järk-järgult keerukaid kujundeid kahemõõtmelises ruumis, st tasapinnal, kuvama. Alles nüüd hakkas kujutatud objektide suuruste ja proportsioonide täpsus tunduma väga ligikaudne.

Aga küsimus, kui korrektselt on figuuri tasapinnal kuvamine ja kui palju need vastavad algsete objektide mahule, sai kunagi väga aktuaalseks. Mingil moel kutsus uus teadusgeomeetria. Täpsem alt on selle sektsioon kirjeldav geomeetria.

Siin ta lihts alt uurib kujundeid ja tasapindu, sirgeid ja punkte, aga ka nende omavahelist suhet – nii kolme- kui ka kahemõõtmelises ruumis.

Konversioonimeetodid

Kujutava kunsti oluliseks tunnuseks on kujundite kuvamine pilditasandil. Lõppude lõpuks on see tegelikult kolmemõõtmeliste ruumiobjektide jäädvustamine kahemõõtmelisuses. Nimelt: kompleks tuleb teisendada lihtsaks ehk objekt, millel on pikkust, laiust, kõrgust, tuleb üle kanda tasapinnale.

Ja kirjeldav geomeetria teeb selliseid "üleminekuid" tänu mõnele meetodile. Kokku on neid umbes kuus. Siin on kolm peamist ja populaarseimat kogu maailmas:

• perspektiiv (kui kujutatud objekt eemaldatakse ruumist);
• ortogonaalne projektsioon (projektsioon paralleelselt, kus kiired on tasapinnaga risti);
• kaldprojektsioon (paralleelprojektsioon, kus kiired on tasapinna suhtes kallutatud).

Kujutatud objekt paistab üsna selgelt aksonomeetrilises projektsioonis (mis hõlmab ortogonaalset ja kaldu). Kuid see projitseeritakse kõige selgem alt ja tõelisem alt, kui seda näidatakse perspektiivis. Ja just ül altoodud meetodid lahendavad suures osas küsimuse, kuidas jooniseid tasapinnal kuvada.

Perspektiiv

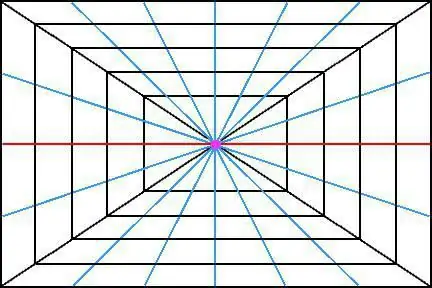
Perspektiiv võtab teiste kuvandimeetodite seas kõige auväärsema koha. Sest inimese silmnagu kaamera objektiiv, näeb see ümbritsevat ruumi sarnaselt. Asjad, mis on vaatlejast kaugemal, tunduvad väiksema suurusega ja mõnikord palju väiksemad kui siis, kui nad on lähedal.

Võtke näiteks ruumis oleva kuubi kujutis. Kui tegelikult on kõik selle servad üksteisega paralleelsed, siis seda objekti eem alt vaadates võib tunduda, et servad koonduvad (või peaksid koonduma) ühes punktis. Ja mis kõige huvitavam, need ei tohiks ühes punktis koonduda, vaid neil peaks olema üks ristumispunkt.

Tänu renessansi meistritele: Albrecht Dürerile, Piero Della Francescale, Andrea Mantegnale, Leon Batista Albertile, teab kaasaegne maal, mis on otsene lineaarne perspektiiv, kuidas määrata horisondi kõrgust ja kaduvaid punkte.

Ja maailmakuulus geenius Leonardo da Vinci vaidles esm alt õhust perspektiivi kontseptsiooni üle. See hõlmab objekti värvi, tooni muutust, selle kontrasti omaduste muutumist (objekti eemaldumisel väheneb).

Ortograafiline projektsioon

Ortogonaalset nimetatakse paralleelprojektsiooniks, mis on suunatud sirgele, mis on tasapinnaga risti. Selle rakendamise käigus jäävad objekti kontuuride mõõtmed muutumatuks. See tähendab, et objekt kuvatakse ilma moonutusteta.

Projitseeritud kolmemõõtmeline objekt on justkui jagatud kolmeks vaateks: küljelt, eest ja ül alt. Ja kõike seda samal ajal vaadates saate lisadaesitus sellest, kuidas objekt mahuliselt välja näeb. Samas jäävad kujundi mõõtmed muutumatuks nii ruumilisel kui ka kahemõõtmelisel pildil.

Kaldprojektsioon

See projektsioon on jagatud veel mitmeks alamliigiks, nimelt:

• isomeetriline vaade;
• dimeetriline projektsioon;
• trimeetriline projektsioon.

Isomeetril on moonutuskoefitsiendid kõigil kolmel teljel (pikkus, laius, kõrgus). See tähendab, et paarikaupa võetud telgede vahelised nurgad on 120 kraadi. Dimeetrilises on moonutused piki 2 telge võrdsed ja kolmas on erinev. Trimeetrilises projektsioonis on kõik moonutuskoefitsiendid (st piki kõiki kolme telge) erinevad.

Pöörlemisvormid

Kui täisnurkne kolmnurk pöörleb piki ühe kahest jalast telge, kirjeldab selle kolmas külg (hüpotenuus) uut kujundit, mida nimetatakse koonuseks. Ja kui pöörate ristkülikut (ruutu) piki selle ühte külge, saate silindri. Kui poolring pöörleb, tuleb välja kera.

Sellest järeldub, et tasandit mööda mingit telge pöörates saame nn pöörlemiskujud.

Nendel kujunditel on pöörlemistelg. See, kuidas nad lennukis välja näevad, sõltub nende paigutusest silmade kõrguse suhtes. Näiteks silindri ülemine ja alumine külg on sisuliselt ringid. Ja kui vaadata neid tasapinnal, näevad nad välja nagu ellipsid.

Kuid ülesanne muutub kuvamisel veelgi keerulisemaksruumikujud tasapinnal, neil on kaldtelg. Sel juhul on oluline, et pöördekehade kontuurid oleksid viimase teljest võrdsel kaugusel.

Natuke chiaroscuro kohta

Chiaroscuro mängib olulist rolli figuuride kuvamisel lennukis. Sest kujutatava objekti maht ei teki mitte ainult joonte, vaid ka valguse ja varju õige jaotuse tõttu selle külgedel. Ja siis tundub see kahemõõtmelise pinna tasapinnal üsna mahukas.

Seega on kujundite kuvamine tasapinnal, nende suuruste määramine, heleduse ja tumedate laikude õige ülekatte omadused tänu ül altoodud meetoditele täiesti võimalikud. Ja mis kõige tähtsam, need on praktikas tõesti tõestatud meetodid, mida kasutavad meie aja juhtivad eksperdid.